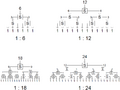
Balancer
Balancer may refer to Load Balancer or Belt Balancer. Splitters are built in a nested way, such that all downstream belts or buildings receive an equal amount of material, regardless if the supply belt is providing sufficient input. A factory that is built this way tends to start up faster, as there is no need to wait for the internal storage to pile up. The size of a balancer grows quadratically as the number of buildings increases.
It is the opposite fill method to the manifold.
Load balancer
A load balancer splits 1:n belts equally (one input belt, n output belts).
Construction
- A Splitter has a single belt input that can split into two or three outputs.
- To make 1:4 or 1:8 balancer, simply nest the 1:2 balancers. To make a 1:9 or 1:27 balancer, simply nest the 1:3 balancers.
- Similar to above, any balancer that can be made from multiplications of two and three can be built. Example, 6, 12, 18, 24, etc.
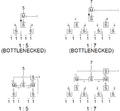
- Balancers with other numbers can be built with simple loop-backs. This loopback will consume some of the belt capacity, reducing the overall throughput. Loop-backs of this sort are necessary for producing fractional splits with denominators that have a prime number composition of values other than two or three. This topic is discussed in detail at Tutorial:Prime splitter arrays.
- Round up the number and build the nearest perfect balancer, then loop back all the unused output.
- In some cases, there may be more than one unused output. Use mergers to combine them into a single belt before loopback.
- To maintain the throughput, the loopback can be split and distributed evenly among the split outputs, using additional splitters and mergers.
- All the above principles apply to balanced Mergers. Just flip the entire setup vertically and swap all the splitters and mergers.
| 1:n | Modified from 1:m | Outputs to loopback | Remarks |
|---|---|---|---|
| 5 | 6 | 1 | |
| 7 | 8 | 1 | |
| 10 | - | - | Split into two, each using 1:5 balancer |
| 11 | 12 | 1 | |
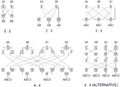
| 13 | 16 | 3 | Combine three unused outputs before loopback |
| 14 | - | - | Split into two, each using 1:7 balancer |
| 15 | 16 | 1 | Alternative to 1:15 split - split into 1:5, then each futher split into three. |
| 17 | 18 | 1 |
Odd-number balancers with loop-back (prime splitter arrays). The top examples have bottleneck problem, the bottom examples don't.
Belt balancer
A belt balancer splits n:m belts equally (n input belt, m output belts).
Construction
A belt balancer can be built by interlacing multiple load balancers such that they have multiple inputs and multiple outputs.
- To maintain the throughput, make sure no segment of the belt is having an item flow rate higher than the capacity of the belt.
- As such, always split before the merge.
Elimination
Whenever possible, avoid the usage of belt balancers. Balancers take up a great deal of space, so it is generally much easier to use another strategy to split up items.
- Consider using manifolds instead, if the total item throughput is within the capacity of a belt.
- Use modular building style for low-compression items, such as Screws and Quickwire. Group them near the buildings that use these ingredients.
- If the output of a building exactly matches the input of another building, pair these buildings up.
- For example, pair an Iron Ingot Smelter with an Iron Plate Constructor or two Wire Constructors with a Cable Constructor.
- If the item flow rates of the incoming belts are known to be equal, there is no need to balance them, regardless if each belt is full or not.
- E.g. two belts carrying 780 Iron Ore each.
Belt compressor
Sometimes it is useful to compress n-number of belts into m-number of full-belts, with the last belt carrying the remainder. This can be applicable to: Mega-factories and compressing from multiple sources (Eg multiple Miner outputs).
- Fluctuating input rates can cause issues with simple belt compressors.
- This mainly happens in recipes that output multiple items at once
- Eg Pure Iron Ingots output 13 items at a time
- The Any lines will fill, and the merger takes from them 50:50
- This incorrectly causes overflow to the top line when space is available at the end of the current load
- This mainly happens in recipes that output multiple items at once
- Buffered Belt Compressors utilize an Industrial Storage Container as a buffered merger
- Consumes a much larger footprint
- Requires 48 stacks to back-fill before overflow line begins
- Has up to 48 stacks of back-fill to ensure main line is adequately supplied
Balancer examples
Perhaps the most important element of factory design in Factorio was balancers. Balancers aren't as critical in Satisfactory for two reasons. The first is that even a massive factory can operate with only a few max-level belts of a single material on the main bus. The second is that Satisfactory machines have much larger buffers on the input and output. This allows for much greater irregularity in belt flow before machines start losing efficiency. That being said, balancers are still important.
The concept of balancers is pretty simple. The output belts should be able to draw from the input belts at any ratio. There are hundreds of ways of configuring these but here are a few examples.
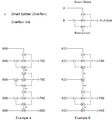
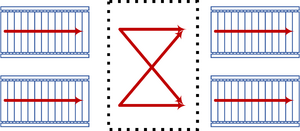
2-to-2 Belts
Definitely the easiest configuration, there is a load of ways to do this one. One possible configuration looks like this. Left shows the first layer, right the second.
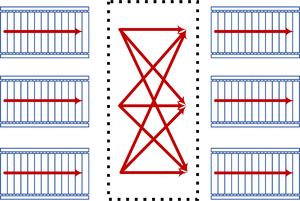
3-to-3 Belts
The unique thing about Satisfactory, when compared to Factorio, is the fact that splitters and mergers operate on a 3-to-1 ratio. This means that, unlike Factorio, 3-to-3 belt balancers are straightforward. An example configuration looks like this with left-to-right showing the build-up of the layers.
Implementation of a 3-to-3 belt balancer.
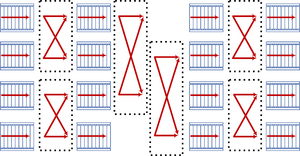
4-to-4 Belts
4-to-4 belts are where balancers get interesting. An example using a grid of 2-to-2s as shown in the schematic on the right.
Alternate Examples:
2-2:
3-3:
4-4:
2-2 Flat -> 2-2 Vertical -> 2-2 Flat
6-6:
3-3 flat -> 2-2 vertical (generally easier and smaller than a 5x5)
9-9:
3-3 Flat -> 3-3 Vertical -> 3-3 Flat
External links
See also
| ||||||||||||||||||||||||||||||||